Project 2
In 2022 as a part of my PhD, I conducted a systematic review and a meta-analysis to determine if there was a bilingual advantage in episodic memory as measured by recognition tasks in paired associate learning tasks. Episodic memory is a type of memory that enables an individual to access mental information about the location and timing of personal events in their life, and is usually assessed by means of two types of measures tapping recognition and recall. In recognition tasks, participants are usually shown words or pictures and asked to decide whether they had already seen the items in the previous trials.
ACTIONS
To conduct a meta-analysis, you need to first identify eligible studies (for this you specify your inclusion/exclusion criteria) and extract the relevant data: effect sizes where available. Where effect sizes are not reported, you extract other values such as correlations, means, standard deviations, t-values, and F-values that enable you to calculate effect sizes yourself. Below, a piece of code in R that I used to calculate effect sizes (Cohen’s d) based the number of participants, means, and standard deviations.
#Calculating an effect size (Cohen's d) for study by Ahmed et al. (2023)
esc_mean_sd(grp1m = 18.12, grp1sd = 1.98, grp1n = 25, grp2m = 13.84, grp2sd = 2.3, grp2n = 25, es.type = "d")
#Calculating an effect size (Cohen's d) for study by Ali & Abdalgane (2023)
esc_mean_sd(grp1m = 16.6, grp1sd = 1.43, grp1n = 30, grp2m = 12.8, grp2sd = 1.38, grp2n = 30, es.type = "d")
META-ANALYSIS RESULT
Twelve studies were included in the final comparison of recognition performance between monolingual and bilingual samples. I had to exclude other studies from this analysis due to comprising bilingual samples exclusively or the lack of information regarding the number or novel words recognised by participants during the testing/assessment of learning.
I then investigated between-study heterogeneity by using Cochran’s Q statistic and I² test. Cochran’s Q statistic revealed a statistically significant difference between the true effect size among the included studies, Q = 22.37, df = 11, p = 0.0217. I² test resulted in a moderate heterogeneity (50.8%) and thus the random effect model was chosen for this meta-analysis. There was a statistically significant effect size observed between the monolingual and bilingual in terms of their Recognition of the novel objects, g = .63, 95% CI [0.45; 0.80], p < 0.001 indicating a bilingual advantage.
#Random-effects model meta-analysis
SMD 95%-CI %W(fixed)
Yoshida, Tran, Benitez, & Kuwabara (2010) 1.2150 [ 0.5382; 1.8918] 6.5
Kaushanskaya & Marian (2009) 0.3976 [-0.1757; 0.9708] 9.1
Kaushanskaya & Marian (2009) 0.8830 [ 0.2661; 1.5000] 7.8
Kaushanskaya (2012) - Experiment 1 0.5868 [-0.0812; 1.2548] 6.7
Kaushanskaya (2012) - Experiment 2 0.4170 [-0.2437; 1.0777] 6.8
Yoshida, Tran, Benitez, & Kuwabara (2011) 1.4629 [ 0.7620; 2.1638] 6.1
Morini (2014) 0.0781 [-0.4121; 0.5683] 12.4
Menjivar & Akhtar (2017) 1.3201 [ 0.5518; 2.0884] 5.0
Warmington, Kandru-Pothineni, & Hitch (2019) 0.3080 [-0.3157; 0.9317] 7.6
Buac, Gross, & Kaushanskaya (2016) 0.3070 [-0.1316; 0.7456] 15.5
Kaushanskaya & Marian (2009) 0.9272 [ 0.3647; 1.4897] 9.4
Hamada & Koda (2011) 0.7885 [ 0.1441; 1.4329] 7.2
Number of studies combined: k = 12
SMD 95%-CI z p-value
Random effect model 0.6310 [ 0.4585; 0.8034] 7.17 < 0.0001
Prediction interval [-0.0694; 1.4305]
Quantifying heterogeneity:
tau^2 = 0.0971 [0.0000; 0.4698]; tau = 0.3115 [0.0000; 0.6854];
I^2 = 50.8% [4.8%; 74.6%]; H = 1.43 [1.02; 1.98]
Test of heterogeneity:
Q d.f. p-value
22.37 11 0.0217
FOREST PLOT SUMMARY
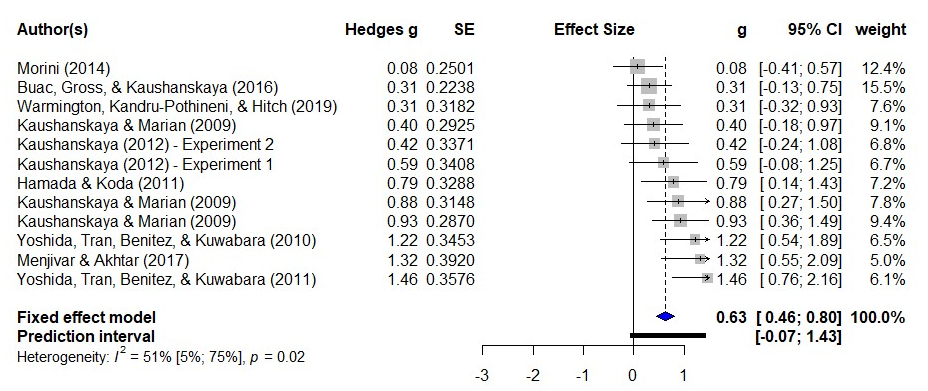
A forest plot is a common way to provide a visual presentation of a meta-analysis.
This forest plot illustrates the differences in recognition of novel words between bilinguals and monolinguals with monolinguals on the left and bilinguals on the right.
The overall effect size depicted by the blue diamond is 0.63 and is considered a moderate effect size. This means that bilinguals were, on average, 0.63 standard deviations more likely to recognise novel words than monolinguals.
There was a significant amount of heterogeneity between the studies, which means that the effect size varied from study to study. This could be due to a number of factors, such as the age of the participants, the type of novel words that were used, and the way that the study was conducted. Despite the heterogeneity, the overall effect size was statistically significant, which means that we can be confident that there is a real difference in recognition of novel words between bilinguals and monolinguals.
SENSITIVITY ANALYSIS
This analysis shows a significant positive effect: The pooled estimate (SMD = 0.63) indicates a significant positive effect, suggesting a moderate difference favouring one group or intervention over another. The I² statistic (50.8%) suggests moderate heterogeneity, meaning results vary somewhat across studies.
Omitting individual studies didn’t substantially alter the overall effect (SMD range: 0.58-0.71), suggesting no single study overwhelmingly drives the results. Additionally, tau² values fluctuated when omitting studies, indicating some studies contribute more to heterogeneity than others. The effect remains significant and positive even after considering the influence of individual studies, supporting its robustness.
#Influential analysis output
SMD 95%-CI p-value tau^2 tau
Omitting Yoshida, Tran, Benitez, & Kuwabara (2010) 0.5904 [0.4120; 0.7688] < 0.0001 0.0858 0.2929
Omitting Kaushanskaya & Marian (2009) 0.6542 [0.4733; 0.8350] < 0.0001 0.1107 0.3327
Omitting Kaushanskaya & Marian (2009) 0.6096 [0.4299; 0.7892] < 0.0001 0.1092 0.3305
Omitting Kaushanskaya (2012) - Experiment 1 0.6341 [0.4556; 0.8126] < 0.0001 0.1141 0.3377
Omitting Kaushanskaya (2012) - Experiment 2 0.6466 [0.4679; 0.8253] < 0.0001 0.1104 0.3323
Omitting Yoshida, Tran, Benitez, & Kuwabara (2011) 0.5773 [0.3994; 0.7553] < 0.0001 0.0606 0.2462
Omitting Morini (2014) 0.7091 [0.5248; 0.8933] < 0.0001 0.0668 0.2584
Omitting Menjivar & Akhtar (2017) 0.5944 [0.4174; 0.7714] < 0.0001 0.0826 0.2874
Omitting Warmington, Kandru-Pothineni, & Hitch (2019) 0.6577 [0.4782; 0.8372] < 0.0001 0.1051 0.3242
Omitting Buac, Gross, & Kaushanskaya (2016) 0.6902 [0.5026; 0.8778] < 0.0001 0.1003 0.3167
Omitting Kaushanskaya & Marian (2009) 0.6002 [0.4190; 0.7814] < 0.0001 0.1066 0.3265
Omitting Hamada & Koda (2011) 0.6188 [0.4398; 0.7978] < 0.0001 0.1126 0.3355
Pooled estimate 0.6310 [0.4585; 0.8034] < 0.0001 0.0971 0.3115
I^2
Omitting Yoshida, Tran, Benitez, & Kuwabara (2010) 48.2%
Omitting Kaushanskaya & Marian (2009) 53.9%
Omitting Kaushanskaya & Marian (2009) 53.9%
Omitting Kaushanskaya (2012) - Experiment 1 55.3%
Omitting Kaushanskaya (2012) - Experiment 2 54.4%
Omitting Yoshida, Tran, Benitez, & Kuwabara (2011) 39.8%
Omitting Morini (2014) 40.4%
Omitting Menjivar & Akhtar (2017) 47.7%
Omitting Warmington, Kandru-Pothineni, & Hitch (2019) 52.9%
Omitting Buac, Gross, & Kaushanskaya (2016) 49.7%
Omitting Kaushanskaya & Marian (2009) 52.8%
Omitting Hamada & Koda (2011) 54.8%
Pooled estimate 50.8%
Details on meta-analytical method:
- Inverse variance method
- DerSimonian-Laird estimator for tau^2
GROWTH/NEXT STEPS
Subgroup Analyses: Explore potential moderators of effect through subgroup analyses or meta-regression.
Sensitivity Analyses: Assess results’ robustness using alternative effect measures or models.


Contact Details
- Email: contact@martacies.com
- Sheffield, United Kingdom